|
For a review of line reflections, see the Refresher section Transformations: Reflections.
Now let's expand that knowledge of reflections in relation to geometry.
 |
A line reflection is a rigid transformation (isometry) that maps every point P in the plane to point P', across a line of reflection, m, such that:
|
Case 1: if point P is ON line m, the
point is its own reflection ( P = P') and
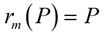 (where point P is "fixed").
|
Case 2: if point P is NOT on line m,
then m is the perpendicular bisector of 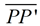 where
|
Note: As shown, when formally defining a line reflection, there are two situations (cases) that need to be considered
for a precise definition. Is the point being reflected lying ON the line of reflection, or NOT ON the line of reflection? |
"A line reflection requires a line and the knowledge of perpendicular bisectors." NGMS
A reflection over line m (notation rm ) is a transformation in which each point of the original figure (pre-image) has an image that is the same perpendicular distance from the reflection line as the original point, but is on the opposite side of the line.
A reflection is called a rigid transformation or isometry because the image is the same size and shape as the pre-image.
|
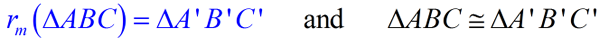
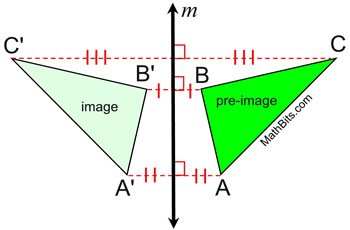 The reflection line, m, is the perpendicular bisector of the segments joining each point
to its image.
Notice that these segments are parallel,
since they are perpendicular to the same line.
|
In this reflection that maps ΔABC to ΔA'B'C', the distances from the pre-image points to the image points vary (are not necessarily equal), but the segments representing these distances are parallel.
Orientation (lettering): The lettering of the points of the pre-image, in this diagram, is clockwise A-B-C, while the image is lettered counterclockwise A'-B'-C'. When lettering changes direction, orientation is not preserved.
This reversal of the lettering directions
is referred to as a non-direct
or opposite rigid transformation (or isometry). |
Properties preserved under a line reflection from the pre-image to the image.
1. distance (lengths of segments remain the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. collinearity (points remain on the same lines)
----------------------------------------------------------
The orientation (lettering around the outside of the figure), is not preserved. The order of the lettering in a reflection is reversed (from clockwise to counterclockwise or vice versa). |
|
|
Since naming (lettering) the figure in a reflection requires changing the order of the letters
(such as from clockwise to counterclockwise), a reflection is more specifically called
a non-direct or opposite rigid transformation.
Line Reflection in the Coordinate Plane:
While any line in the coordinate plane may be used as a line of reflection,
we will limit the lines to be vertical, horizontal,
or bisecting the quadrants through the origin (y = x or y = -x).
You can see examples of these choices on the Refresher page
Transformations: Reflections.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
